VAR分析の理論および特徴

VAR分析モデルでは、ある時間軸に沿って集められたデータを基に定式化が行われます。その際、利用される変数間にある関係性について、同時点のみならず、各変数のラグ変数（変換間に生じる影響が同時的に発生せず、次期に遅れて影響を示す変数）間にある関係性、つまり過去時点も加えて立式することに特徴があります。
VAR分析モデルについて観念的に示せば、＜図1＞の通りになります。

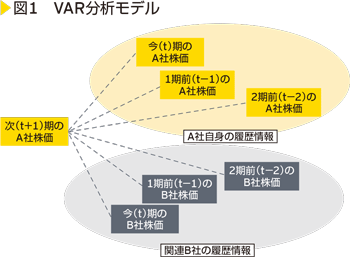
A社の将来株価をVARモデルにより予測する目的で、A社と関連するB社に着目すると仮定します。A社の株価に影響を与える変数として、A社自身の履歴情報、関連B社の履歴情報が想定される場合、定式化が可能となります。ここで履歴情報とは、過去の各社株価データを示しております。
統計的手法を用いて、何期前までのラグ変数を用いるか検証することも可能ですが^※1、簡易に次期（t＋1）・今期（t）・前期（1期前（t－1）、2期前（t－2））を想定するとしましょう。つまり、この場合の株価予測モデルでは、次期（t＋1）のA社株価を予測するために、今期（t）のA社株価、1期前（t－1）のA社株価、2期前（t－2）のA社株価、今（t）期のB社株価、1期前（t－1）のB社株価、2期前（t－2）のB社株価を変数として選択します。数学的な表現をすれば次式の通りです。

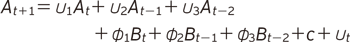
AはA社株価、BはB社株価、添字tは期、cは定数項、uは攪乱項ないし誤差項、各υ及びおよびΦは推定パラメータを示すモデル式となります。

こうしたVARによる時系列分析が開発された背景には、2011年にノーベル経済学賞を受賞したクリストファー・シムズによる有名な「シムズ批判」に言及する必要があります。シムズの見解は、あらゆる経済理論を前提とするモデルでは、恣意（しい）的にモデルが設計される余地があり、正確なパラメータの推定ができないというものです。通常、経済理論モデルでは、複数の均衡式を前提として構造的に定式化を図りますが、その際に利用する変数に次のバイアスが生じます。一つは、既存の理論は、主観的に前提としているにすぎないために、恣意性が完全には排除できないというバイアスであり、もう一つは、定式化する際に内生変数が同時的に決定されるという仮定が置かれていることから推定パラメータに識別の必要が生じるというバイアスとなります。
そこでシムズが提唱したアプローチが、このVAR分析モデルとなります。特に同分析モデルは、伝統的な経済理論モデルと異なり、時系列データから構築される数理統計モデルであるという点に優位性があります。それは、前者が分析段階で一定の主観の下、外生変数・内生変数の区別を必要とするのに対し、後者がこれらを無差別に、純粋に時間的関係性から定式化できるという点です。
つまりVAR分析モデルでは、経済理論をある種の恣意性を孕（はら）む制約的な与件として認識し、これを排除する目的で、変数間の時系列関係からのみ定式化を図っているのです。
もっともこうした理論的想定を排除してしまうことで、モデルの解釈が困難になるという点を批判する見解もあります。しかし、数理統計学に立脚したこの多変量自己回帰過程を前提とするモデルの客観性は大きな利点となるため、経済理論モデルとVAR分析モデルを目的に応じて選択することが望ましいでしょう。さらに近年では経済理論を部分的に内包したVARモデルが構築される等、両見解が組み合わされることでより詳細な予測モデルが開発されている段階にあるのです。

VAR分析モデルは従来の経済モデルとは異なるアプローチでありながら、上述した株価予測といったファイナンス領域、金融政策等の波及的影響を推計する経済政策領域といった分野で、すでに実務レベルで多用されています。またこの他にも、時間の進行に伴って生じる確率過程について同分析モデルが利用できるため、経済分野のみならず、風速予測や希少資源の量的推計といった自然科学分野で広く使用されております。
時系列関係から設計されるVAR分析の多方面での利用可能性を鑑みれば、既存のアプローチとは異なる新たな視角が得られるとともに、客観性の高い予測モデルの設計というニーズに応えることが可能となることでしょう。

2021年2月号では、VAR分析の実務面での取扱いについて解説します。